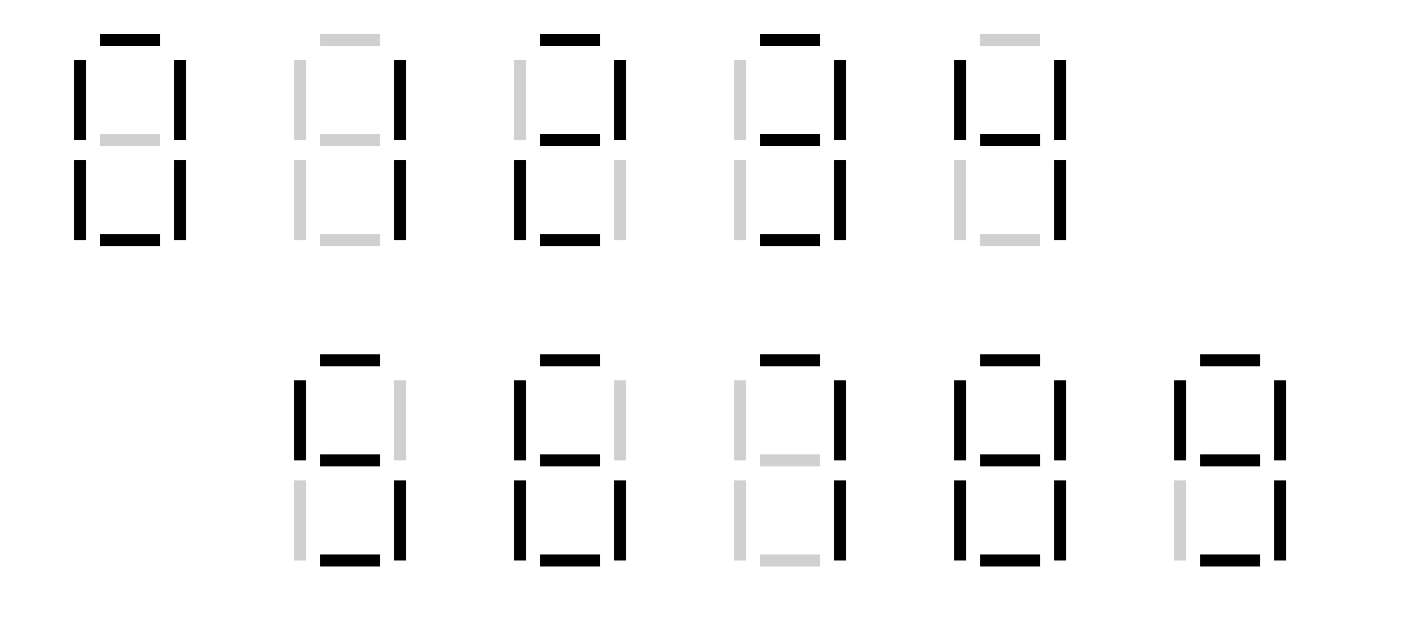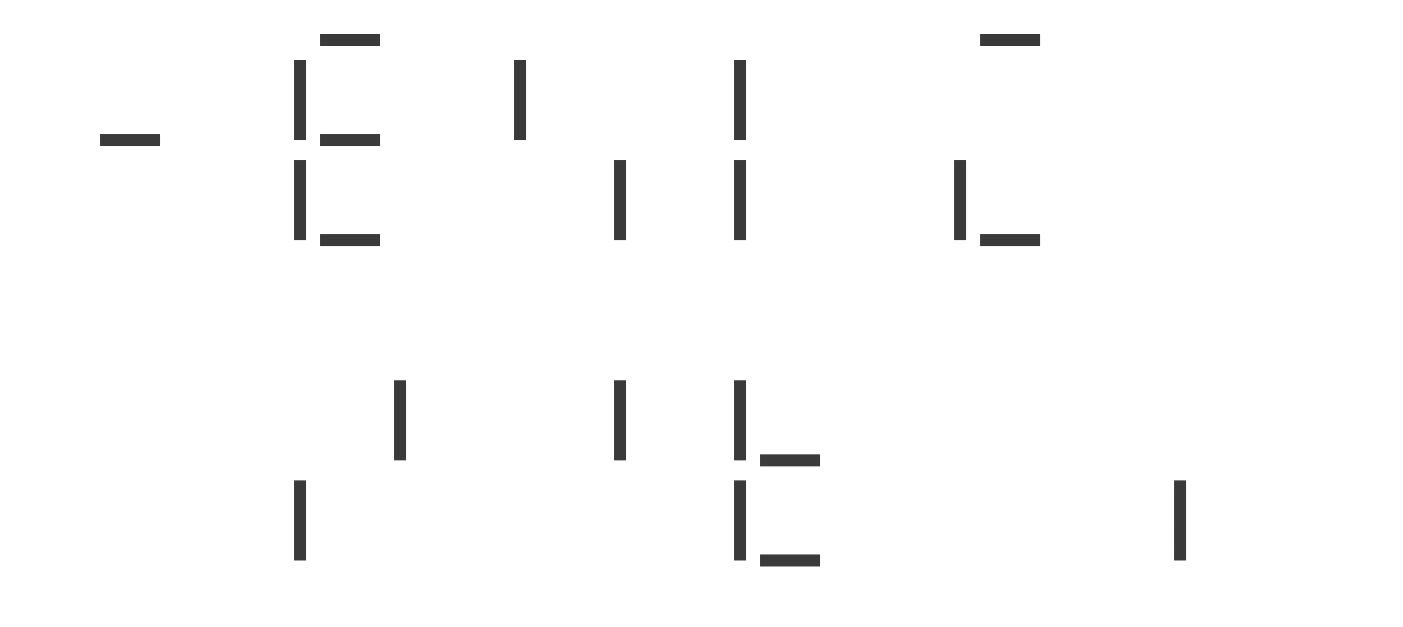破损的红绿灯：数字码的冗余

每次等红灯都会想到这个问题，不妨来研究一下。

红绿灯的数字码

红绿灯的数字显示由 7 条 LED 灯实现，可以显示 0 到 9 的数字。

红绿灯使用的数字码

在不同的显示设置下，它还可以用于显示字母 A 到 H，以此表示超过 99 秒的等待时间¹。

问题在于，红绿灯显示在户外经过风吹雨打，难免会发生故障，而这样的数字编码方式是否有足够的冗余度，可以在数条 LED 故障时依然可以辨认 0 到 9 的数码？

辨认一位数字

对于每一位数字，有 10 中可能状态需要判断。为此，我们至少需要 4 条正常工作的灯条。这是因为每条灯条只有「亮」和「灭」两种状态，于是

\[2^3\gt10\gt2^4,\]

所以，3 条灯条是不够的。

但这只是理论的下界，对于我们讨论的特定情况，我们还不确定 4 条是不是足够。

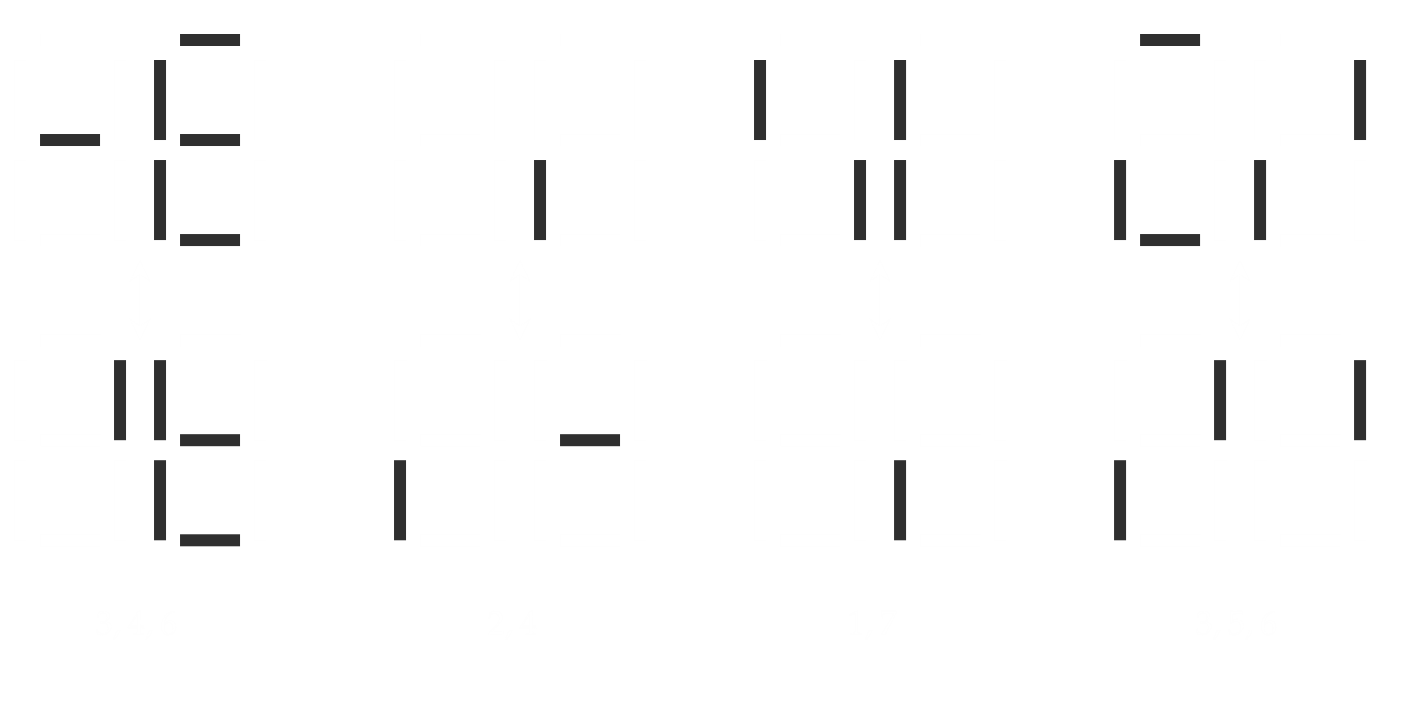
最简单的一种判断方式就是：如果两个数字码之间 只相差一根灯条，那么这根灯条就必须是好的，否则我们将无法区分它们。我们可以将这样的数字码列出来。

相差一根灯条的各个数字码

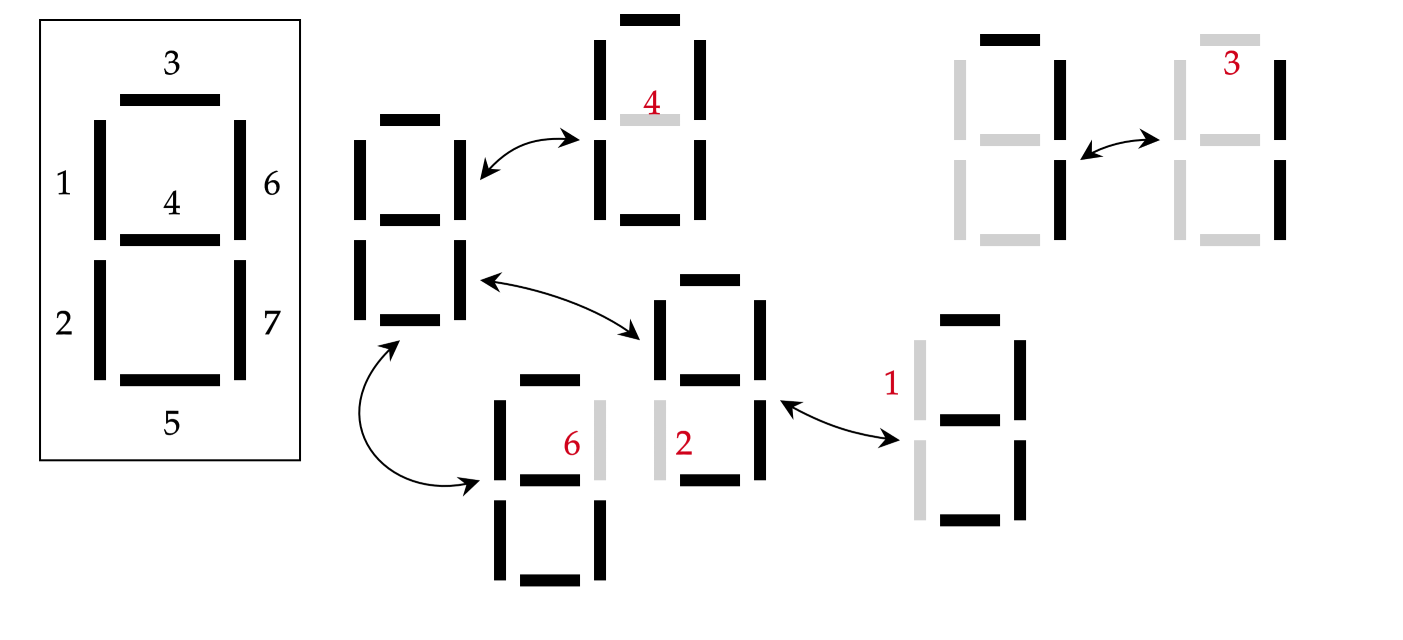
在这里，为了方便讨论，我们给每根灯条都标注了一个编号。可以发现，1、2、3、4、6 号灯条都必须是正常的，因此，至少需要 5 条正常工作的灯条，我们才能正确辨认出这 10 个数码，换言之，只有右下角的 5 号和 7 号灯条可以有出故障的余地。这个冗余显然比理论允许的最大值要小很多。

多等一等：辨认两位数字？

接下来我们可以考虑一个更有意思的问题：由于等红绿灯的时候，数码总是按顺序出现（毕竟是倒计时嘛），假设我们多等一秒，看到了两位连续的数码，则最少需要多少根正常的灯条才可以判断出这两个数码呢？

换句话说，假设我们看到 (0,1)、(1,2)、……、(8,9)、(9,0) 之中的某一组数码，需要多少条好的灯条才能判断出是哪一组呢？

同样从理论最值来说，我们发现只要两根就具有足够的信息量

\[(2^2)^2=16\gt10.\]

但这也只是理论的最值。

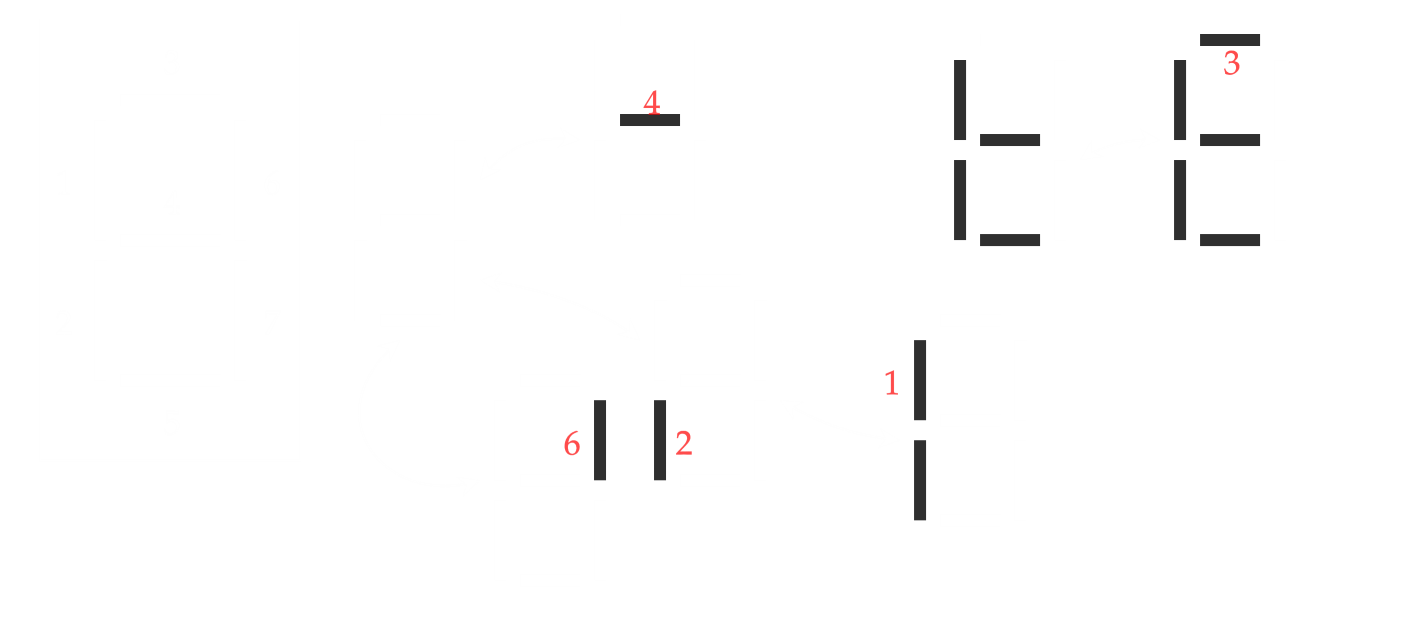
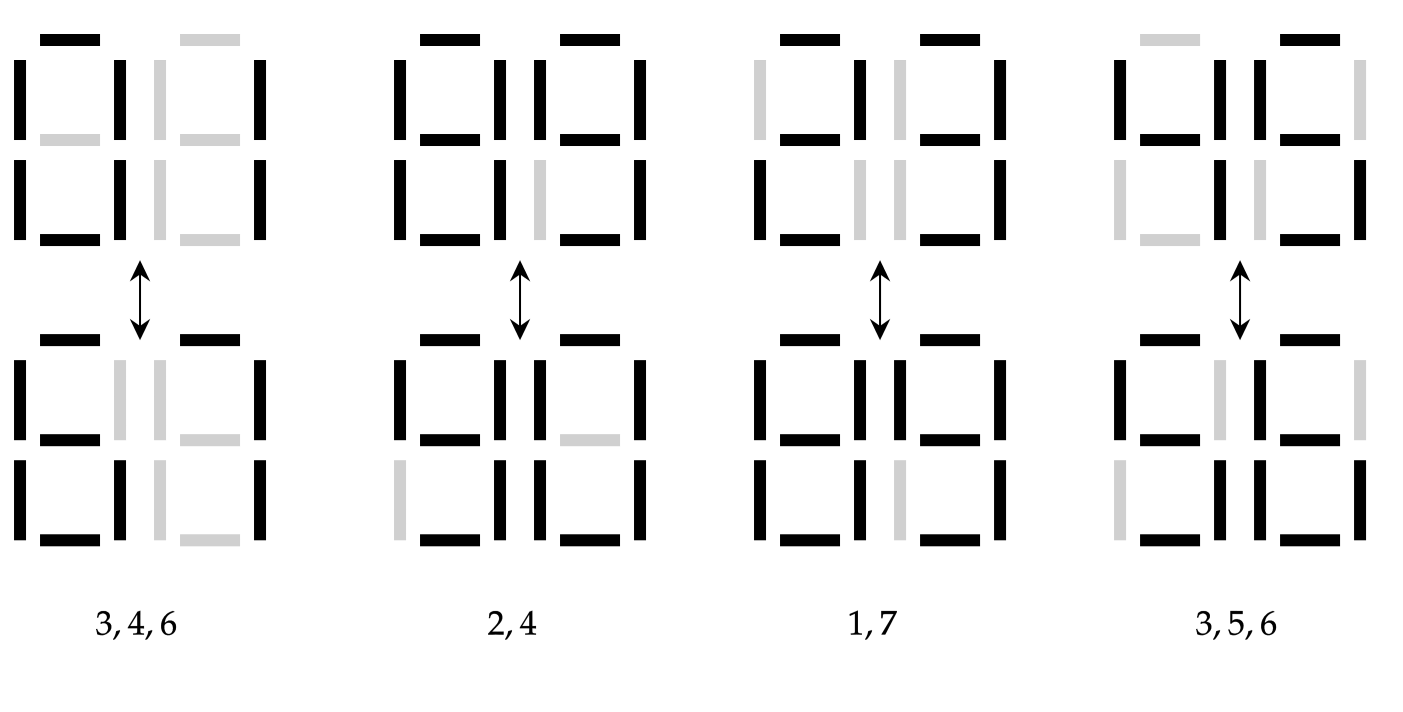
用和刚才相似的思路，我们可以给出一些必须正常工作的灯条。例如：由于 0 和 6 相似，而 1 和 7 相似，则为了区分 (0,1) 和 (6,7)，3、4、6 号之中必须至少有一个正常工作的灯条。用这种方法，我们可以给出如下约束

几组例子给出的约束

从中不难发现，至少需要 3 根正常工作的灯条才能同时满足这些条件。因此，即使是在辨认两位数字的任务下，数字码的设计也同样缺乏足够的冗余。

1. 至少在我家那边会这样显示 ↩